
あのアインシュタインも絶賛する「複利の効果」とは一体、何?
そんな疑問に関して勉強をしますね!
では、今日も勉強のスターート!
アインシュタインが絶賛の複利効果
「複利は人類による最大の発明だ。
知っている人は複利で稼ぎ、知らない人は利息を払う
(“Compound interest is man’s greatest invention. He who understands it, earns it. He who doesn’t pays it.”)」。
この一言を残したのは、いったい誰でしょう。
相当な金融のプロのようにも思えますが、ウォーレン・バフェットでもジョージ・ソロスでもありません。
実は、相対性理論を発見したアルバート・アインシュタイン博士です。
エネルギーの大きさは物質の質量に光速の2乗をかけたものに等しい(E=mc2)ことを発見した博士は、1916年にこの言葉を残したとのことですが、彼にとって複利効果は相対性理論を凌駕する大発見だったのかもしれません。

福利効果とは?
複利効果とは、運用益を再投資することで利益が増幅していく効果のことです。
この金利には「単利」と「複利」の2種類があり、性質が大きく異なります。
まず単利ですが、商品に投資した元本に対して付加される金利のことです。

※500万円を元本として金利3%で運用した場合
運用実績は元本に反映されず、常に同じ金額の元本に対して利息が付く仕組みになっています。そのため、毎月同じ金額が上乗せされます。
一方の複利は、投資によって得た運用益を組み入れた元本に対して付加される金利のことです。
着実に運用益を生み出していれば、それに比例して元本もどんどん増えていくので、同じ元本・利回りで運用した場合、単利よりも資産を増やすことができます。

※500万円を元本として金利3%で運用した場合
複利の計算方法
複利を利用して最終的に自分の資産がいくらになるのかは、次の公式で計算することができます。
元金×{(1+年利)}年数の累乗
「元金」とは、運用や借り入れをする際の元となる金額です。
また、「年利率」とは、1年あたりの資産の増える率のことです。
公式を使って計算してみましょう。
【元金100万円、年利3%、30年間複利運用した場合】
100万円×(1+0.03)30=242万7262円(元金+利息)
242万7262円-100万円=142万7262円(増えた利息)
元金は100万円なので、30年後に受け取れる利息の総額は142万7262円となります。
ちなみに15年後の利息の総額は55万7967円。
15年から30年の間で利息の総額が2倍以上に増加していることがわかりますね。
このように、複利で長期運用をすると、加速度的に資産が増えていきます。
複利は効果的な運用方法だといますね。
(参考:知ってナットク「複利の魅力」 | B.貯蓄する | 一般社団法人 全国銀行協会)
3%と5%で資産が増えていく場合は、5%の方が利回りが大きいため、資産を大きく増やしやすいです。
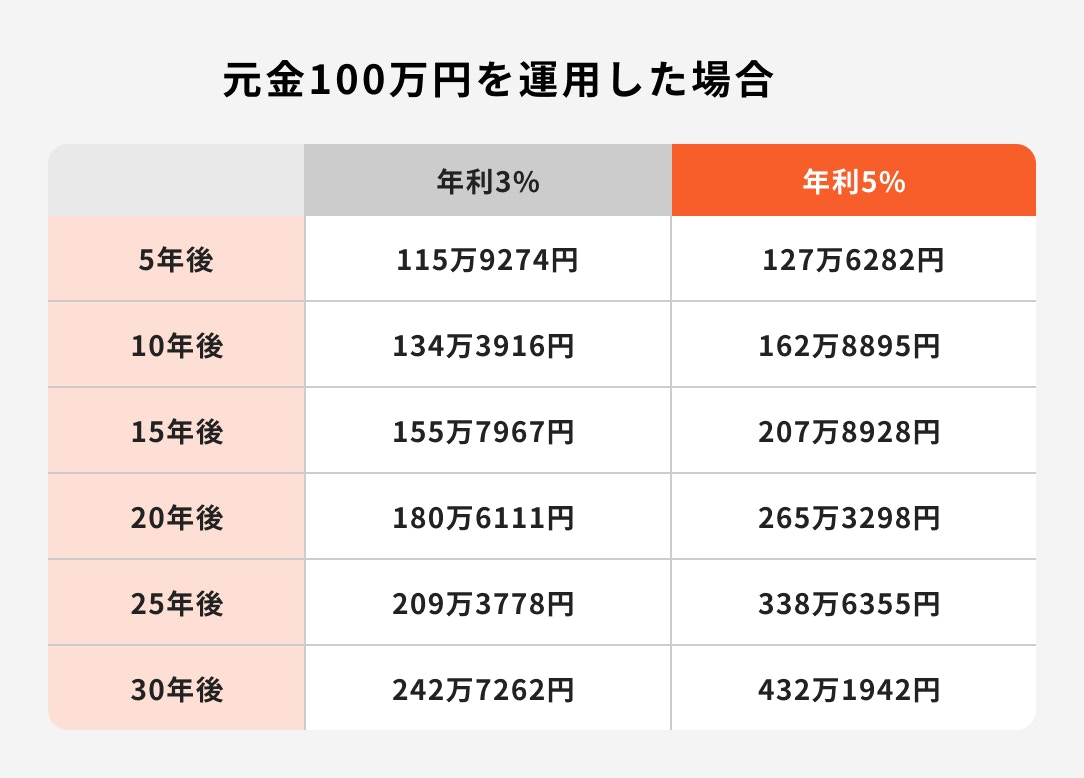
金利の違いで生じる利息の差を比較すると、5年後は10万円程度しか差がありませんが、30年後には約200万円と大きな差になっています。
【オススメサイト】
金融庁サイトで簡単複利の計算!
福利効果は金の卵を産むニワトリ
金の卵を産むニワトリをご存知でしょうか?
例えば、1羽ニワトリが卵を産む。
その1個からひなを育てば2羽になり、それを繰り返すことで、卵が驚くほど増えていくというものです。
お金にも同じことが言えます。
ぜひ、金のニワトリについて、学んでみませんか?
お金が2倍になるには
資産を増やしていくうえでおさえておきたいのが「72の法則」です。
お金が2倍になる期間が簡単にわかる便利な算式。 「72÷金利≒お金が2倍になる期間」となる。 例えば、金利18%でお金を借りた場合、「72÷18=4」となるので、約4年で借りたお金が2倍になることがわかります。
72の法則を詳しく知りたい方は、こちらです。
福利効果を動画で観る
【複利の効果を動画で説明】
バフェット太郎の投資チャンネルより引用
【豆知識】お金とは何?
そもそもお金とは何?
お金の歴史を知れば、お金をもっと深く理解できますよ。
この記事を読んであなたもお金の歴史マニアになりませんか?
【このブログ記事を書いた人の自己紹介】






